Формирование алгоритмического мышления с использованием динамических опорных сигналов

Современные компьютерные технологии позволяют не только по-новому организовывать процесс обучения, но и создавать новый обучающий контент, чему пока уделяется недостаточное внимание. Приведены два примера такого контента, созданного для формирования у обучающихся трудновоспитуемого алгоритмического мышления. Использование языка программирования НТML5 позволяет выполнять эти обучающие программы даже на мобильных телефонах.

Технология без преподавательских подходов – телега впереди лошади. Таким тезисом можно охарактеризовать существующее в настоящее время положение с применение компьютерных технологий в обучении. Записи лекций, обучающие видеоролики – большинство из них опирается на СЛОВО.  Но современные компьютерные технологии позволяют создавать динамическую когнитивную компьютерную графику, моделировать не только реальные физические, но и абстрактные модели, существенно облегчать  трудный процесс понимания с использованием не только левого, но и правого полушария мозга.

«Лучше один раз увидеть, чем сто раз услышать» (или прочитать). Этим приёмом  я и поясню суть методического подхода, разрабатываемого мною с 1993 года и опирающегося на  [1, 2]. Бурное развитие компьютерных технологий дало второе дыхание его применению, так как позволяет работать с обучающими программами на основе этого подхода даже на мобильных телефонах [3-6].

Первый пример — педагогическая модель  алгоритм нахождения максимального элемента одномерного массива.

На экране работают одновременно несколько моделей.

Одна из них — модель времени между двумя последовательно выполняемыми действия алгоритма. По нажатию кнопки  «далее» это время задается только обучающимся, зависит только от его ощущения усвоенности многоплановой информации, не зависит никак от скорости работы компьютера.

Вторая  — модель последовательного выполнения шагов алгоритма  Выполняемое действие маркируется на представленной схеме алгоритма.

Для данного примера самой существенной моделью является авторская когнитивная графическая метафора для выполнения действия сравнения двух значений : заданные по датчику случайных чисел значения элементов массива интерпретируются соответствующими диаметрами шариков, которые помещаются на рычажные качели и по положению качелей определяется, какой элемент «тяжелее».

Ещё одна модель — модель переменной как места для хранения порции информации (именем обладает только МЕСТО для хранения информации, сама информация имени не имеет: недаром  Э. Дейкстра утверждал, что тот, кто осознал, что в программировании используются переменные, понял сущность программирования). Место для претендента, место для чемпиона – эти модели позволяют обучающемуся исправить наиболее часто встречающуюся у них ошибку сравнения двух соседних элементов массива.

Ещё одна модель – словесное описание шагов алгоритма в окне педагогического комментария. В окне педагогического комментария может помещаться и более сложная информация, что будет продемонстрировано на следующем примере.

Когнитивной сложностью данного алгоритма является  сравнение претендента с изменяющимся критерием сравнения, который к тому же является в конце концов выходной информацией. Для понимания этой сложности  полезно сравнение данного алгоритма с алгоритмом подсчета количества положительных  чисел (внешний постоянный критерий сравнения).

Программа позволяет при динамическом характере представления информации сравнить разные её формы  — в виде алгоритма,  графической модели исполнения и педагогического комментария, что способствует глубокому усвоению обучающей информации.

Посмотреть программу в работе можно здесь.

На рис.1 приведена часть последовательности обучающей программы для понимания существа алгоритма нахождения максимального элемента одномерного массива.

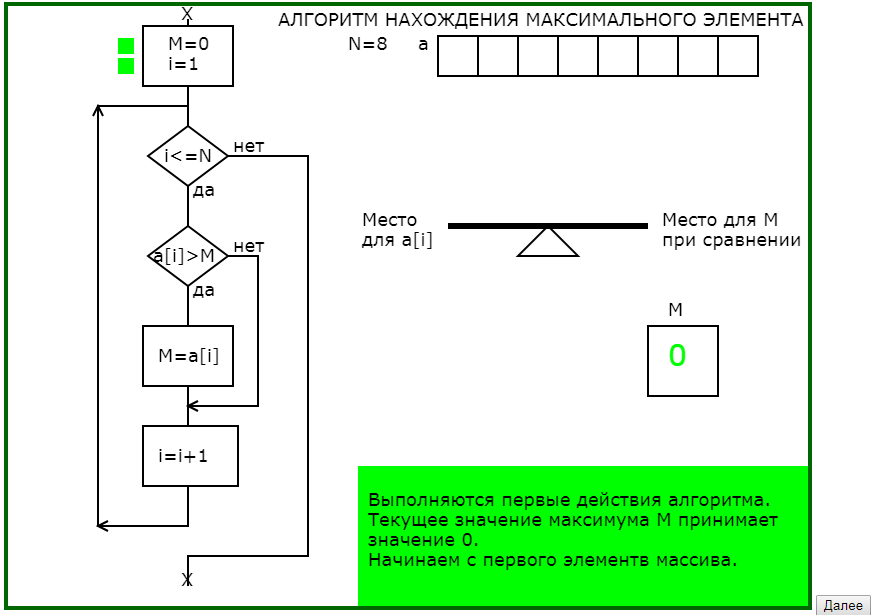
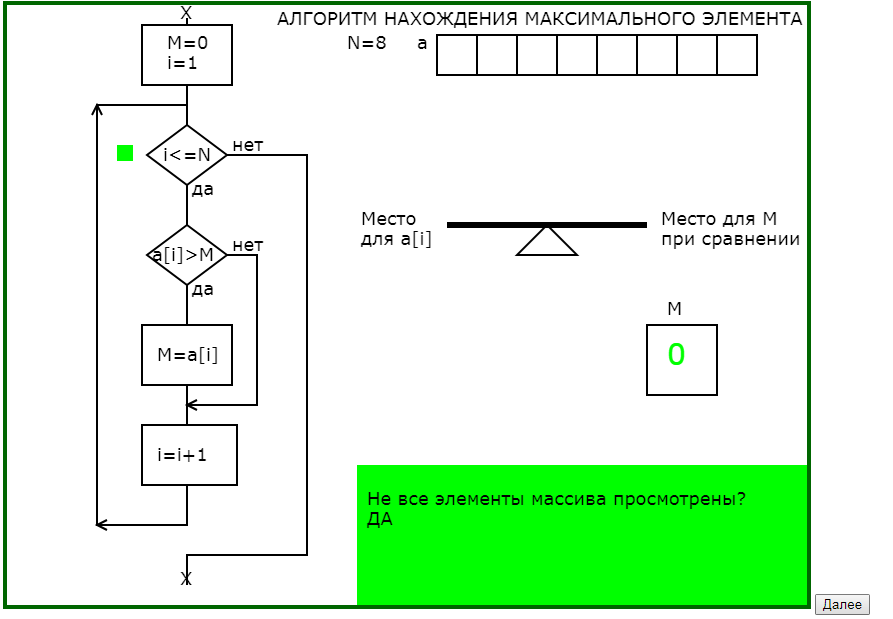
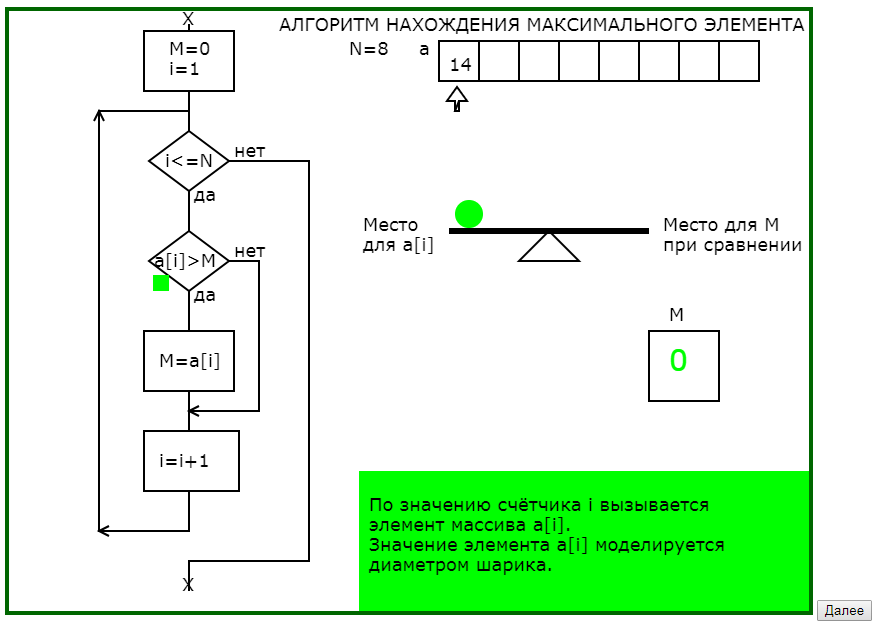
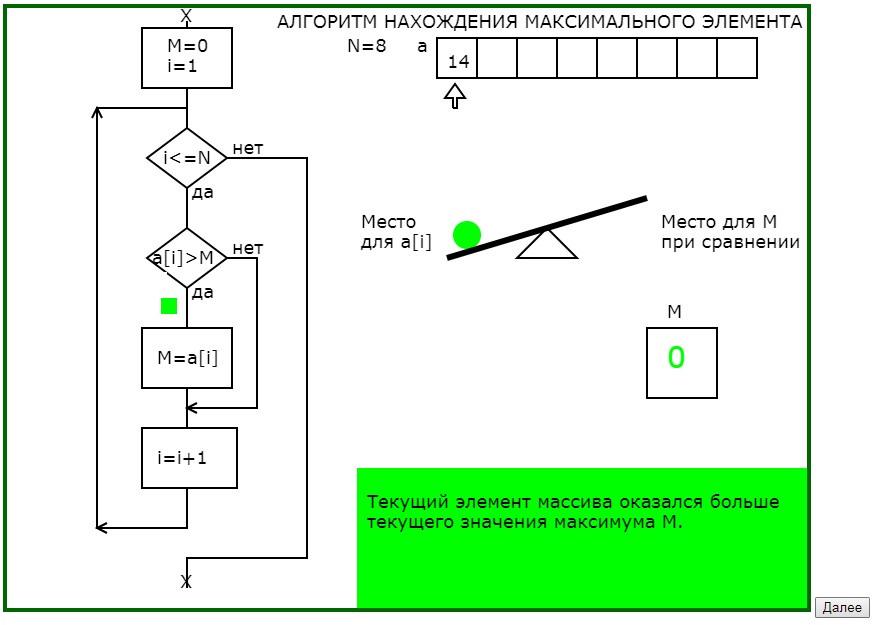
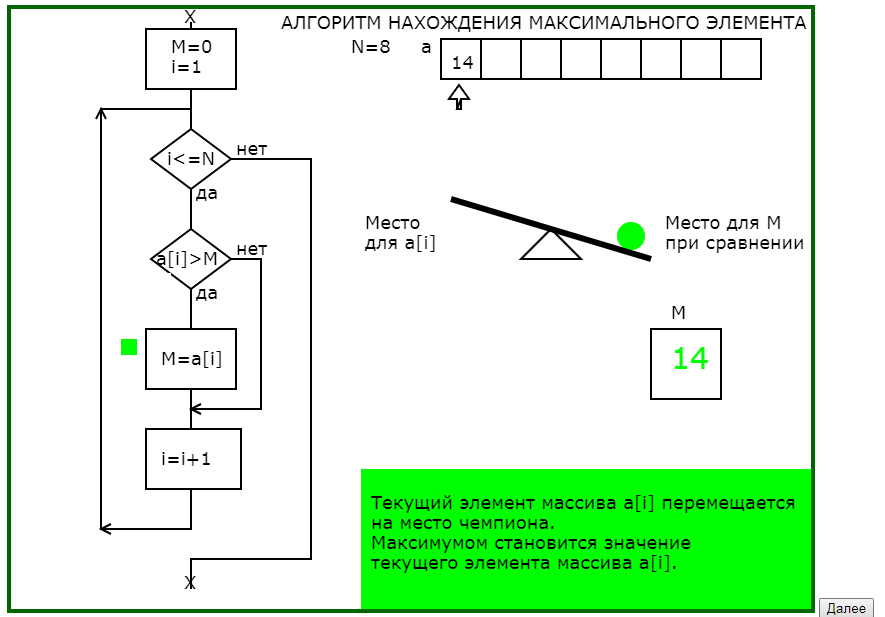
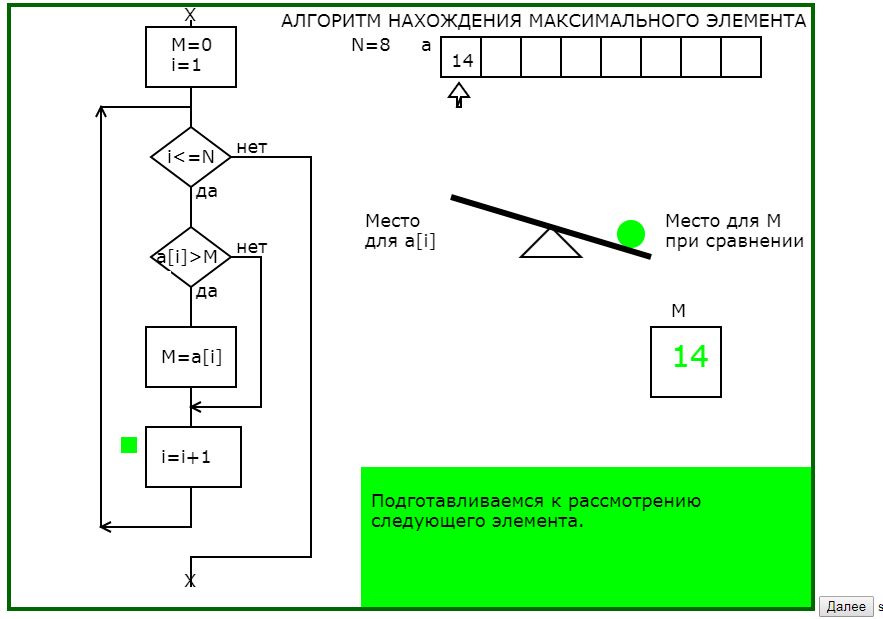
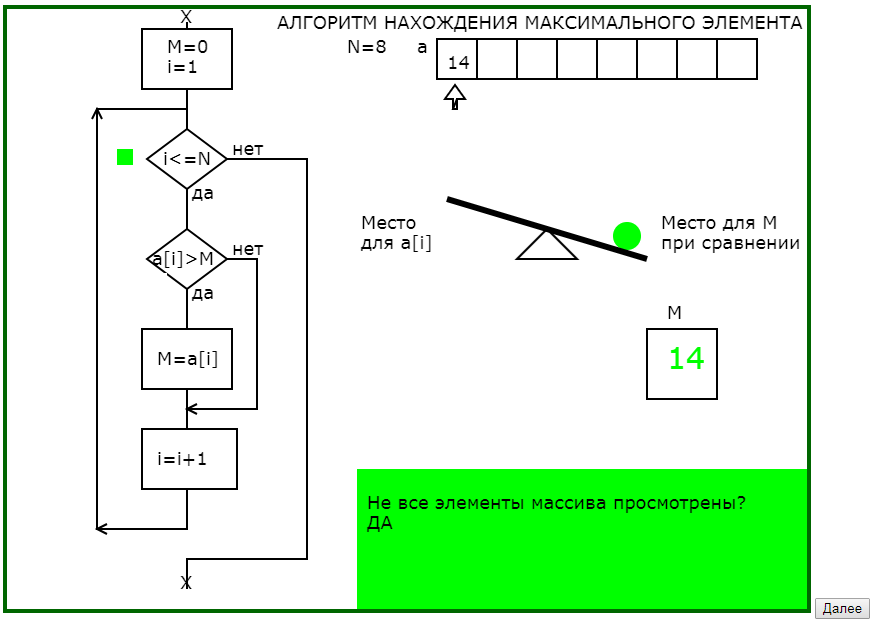
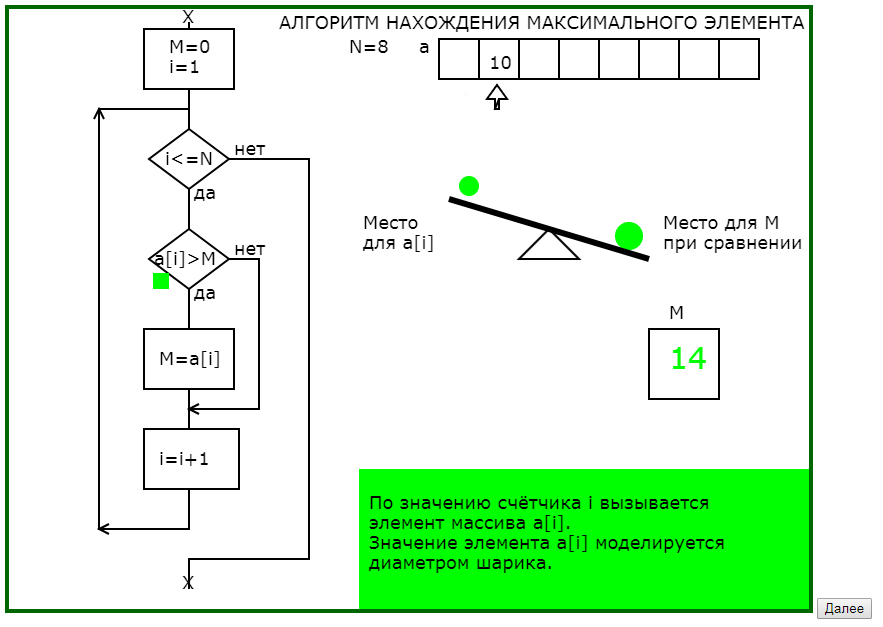
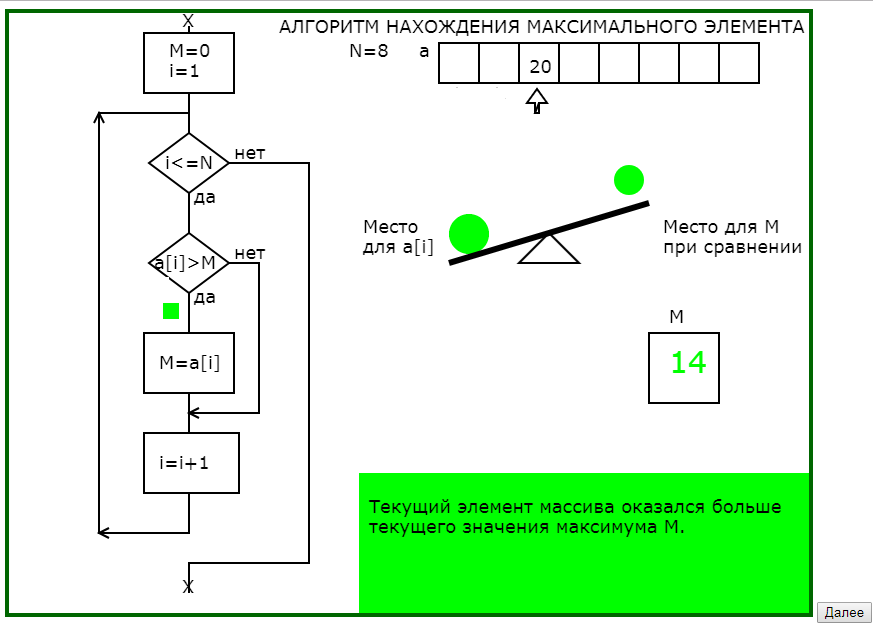
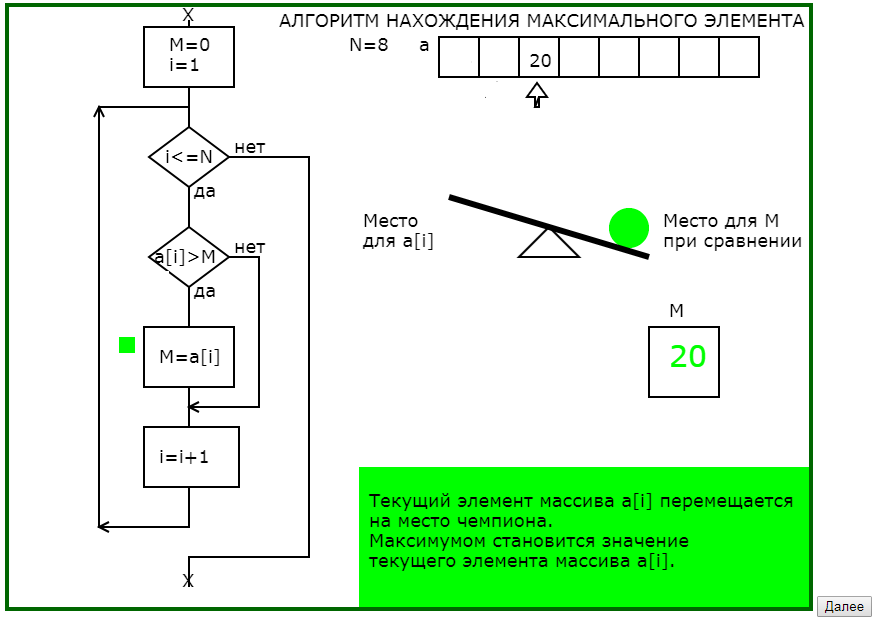Рис.1. Последовательность кадров обучающей программы
«Алгоритм нахождения максимального элемента одномерного массива»

Вторым примером использования динамических опорных сигналов является программа, поясняющая принцип работы алгоритма формирования списка отличников при известных оценках и фамилиях обучающихся.

Отличительной особенностью этой программы является использование  окна педагогического комментария не только для словесного описания действий алгоритма, но и для подсказок направляющих мысль обучающегося.

В предварительных окнах педагогического комментария показывается необходимость тщательного проектирования промежуточной информации, что обычно вызывает затруднения и непонимание, а также показывается возможный результат пренебрежительного отношения к тщательной разработке информационной модели алгоритма.

Программа графически с соответствующим педагогическим комментарием в 4 этапа моделирует процесс заполнения массива фамилий отличников (что на языке программирования записывается в одном действии присваивания), раскрывая и сложности,  и возможности алгоритмических действий.

Смотрите программу в работе по этой ссылке.

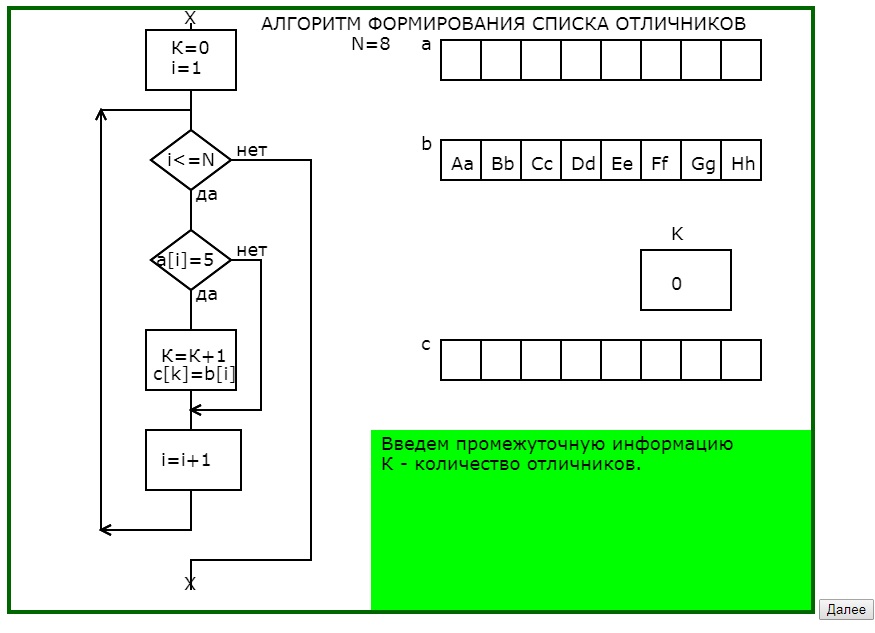
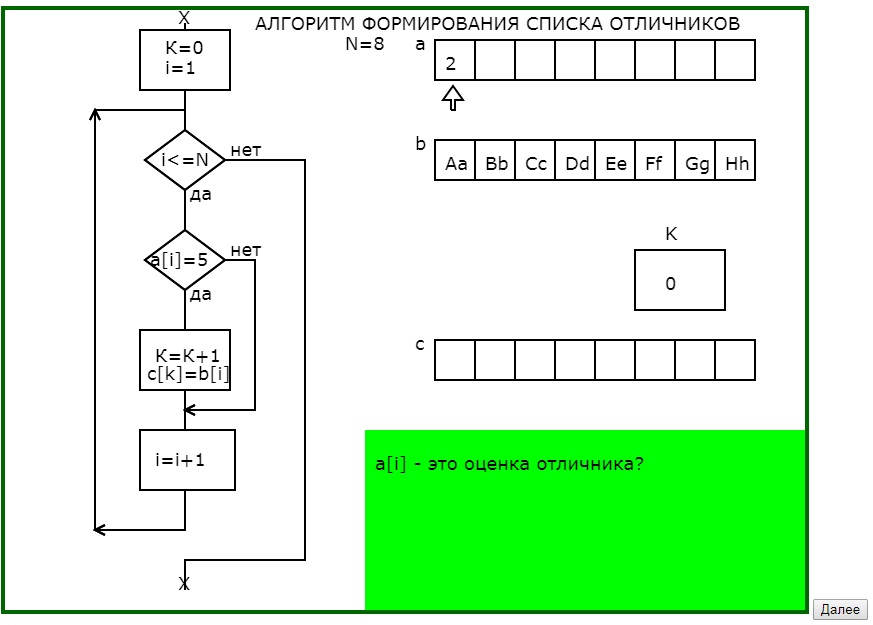
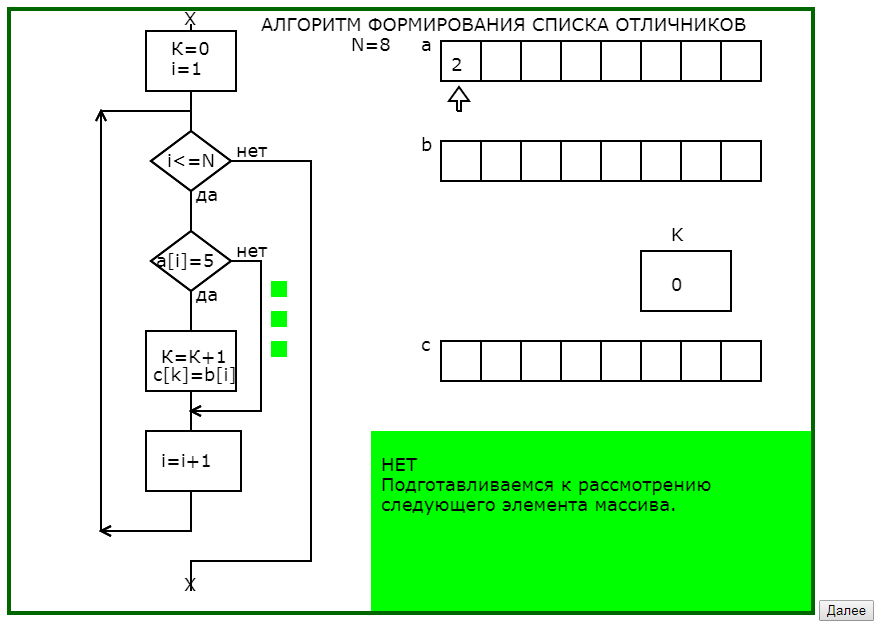
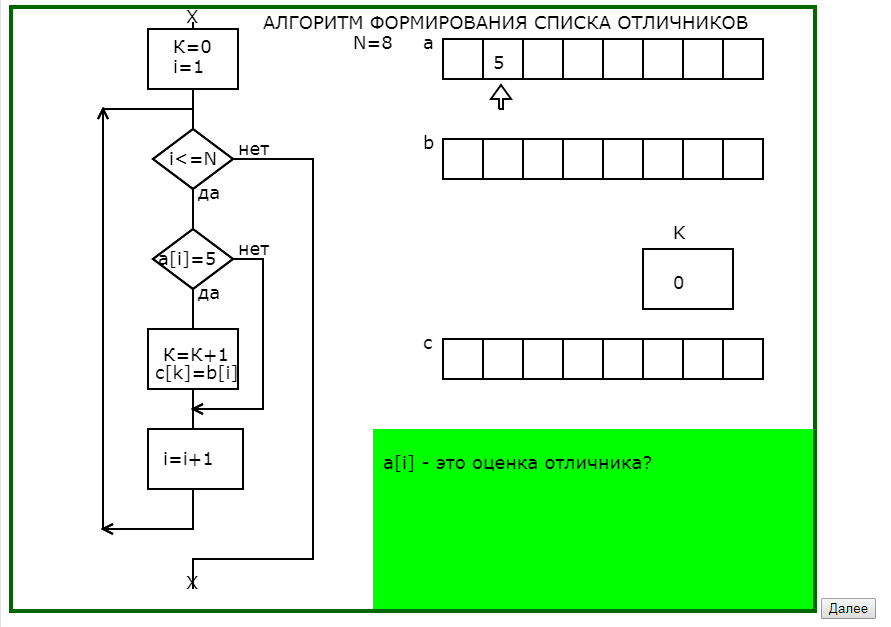
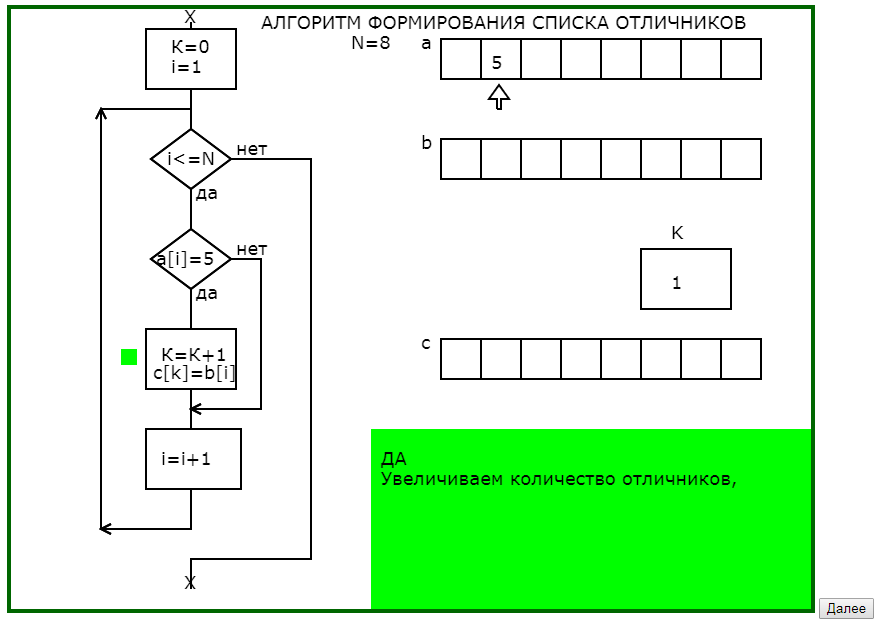
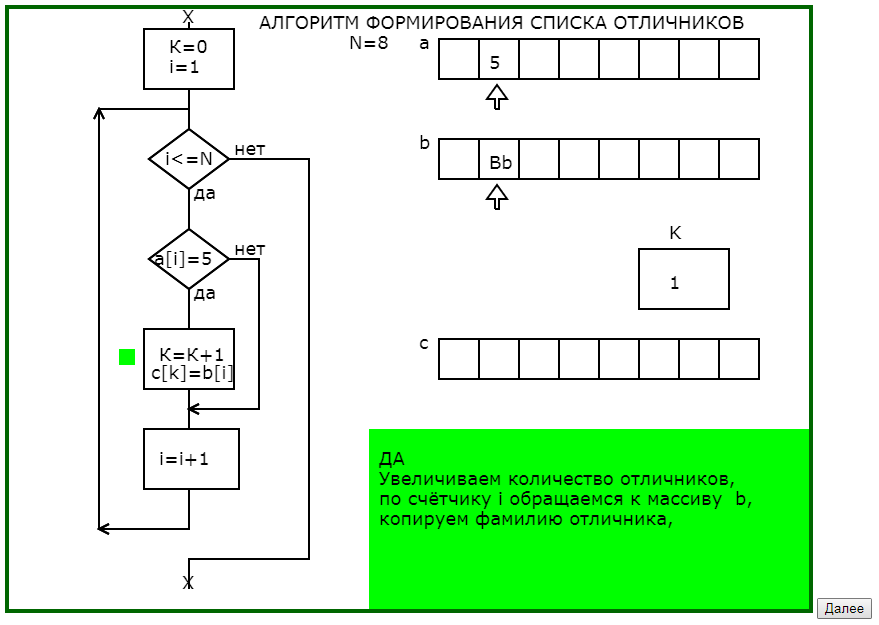
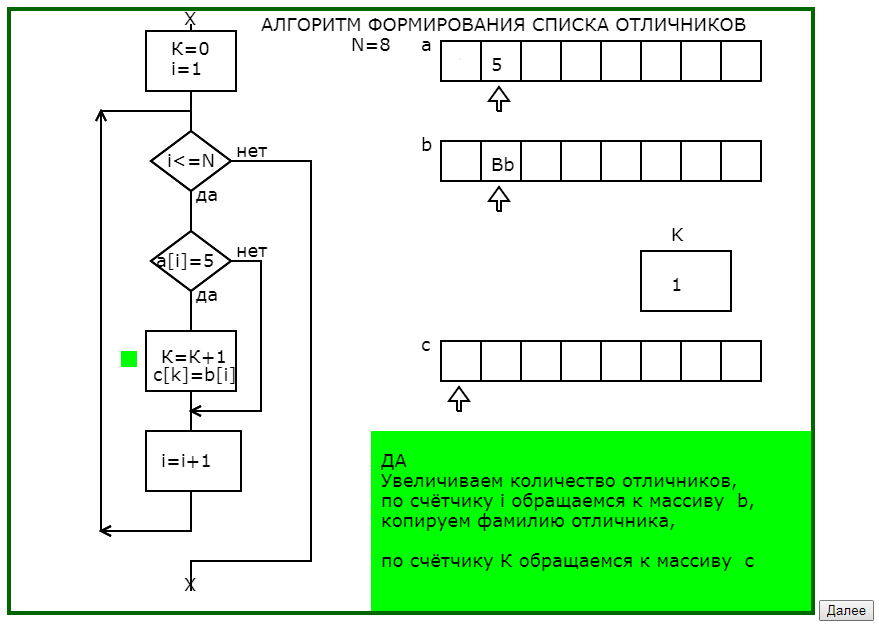
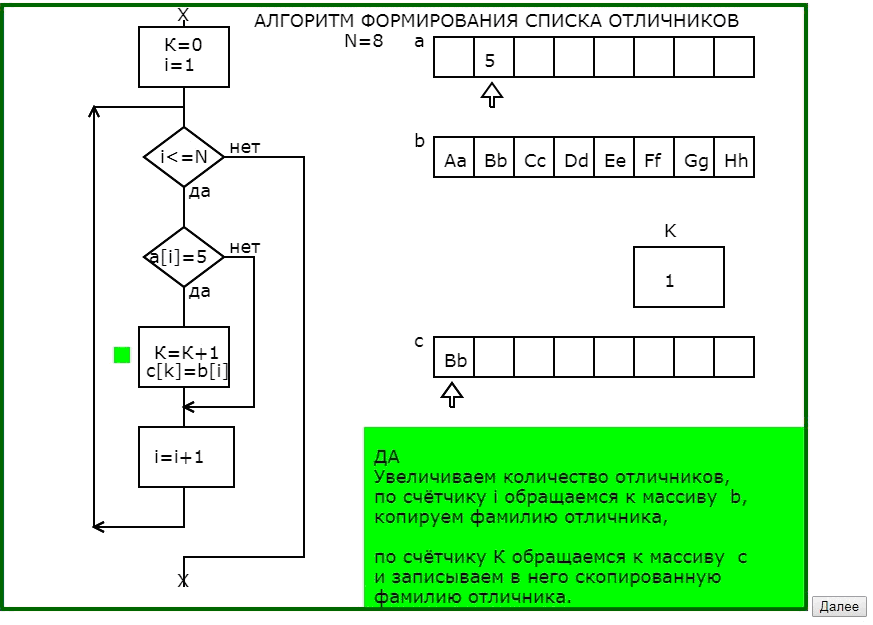
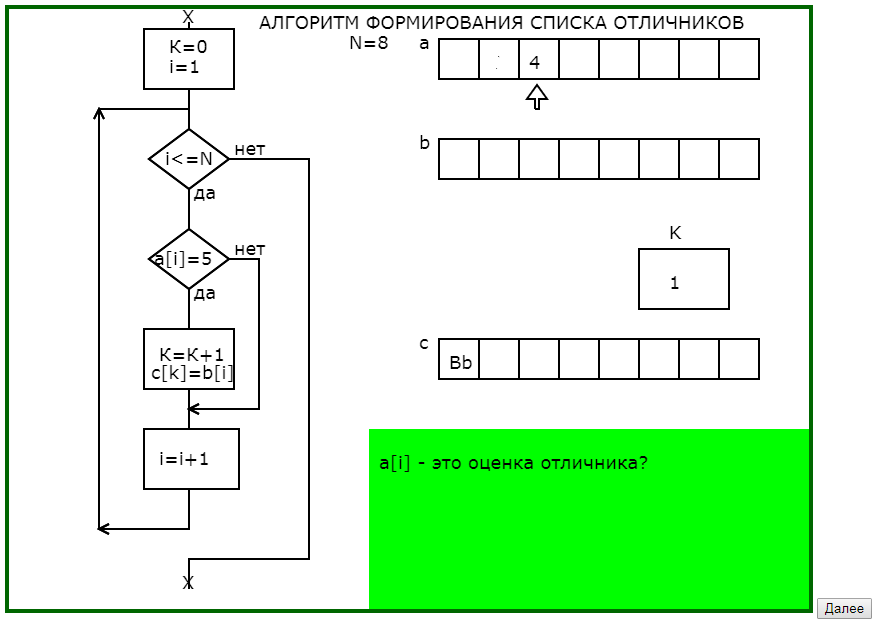
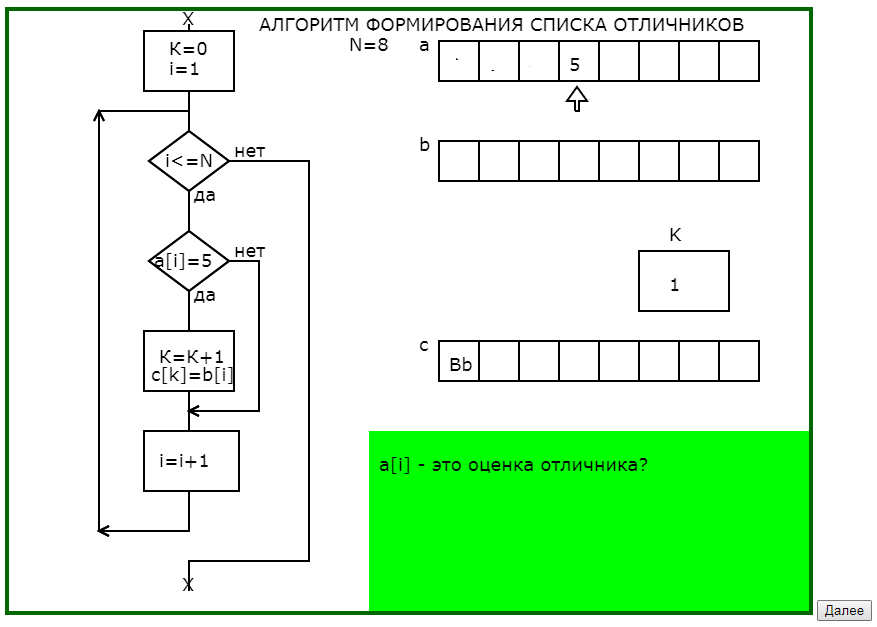
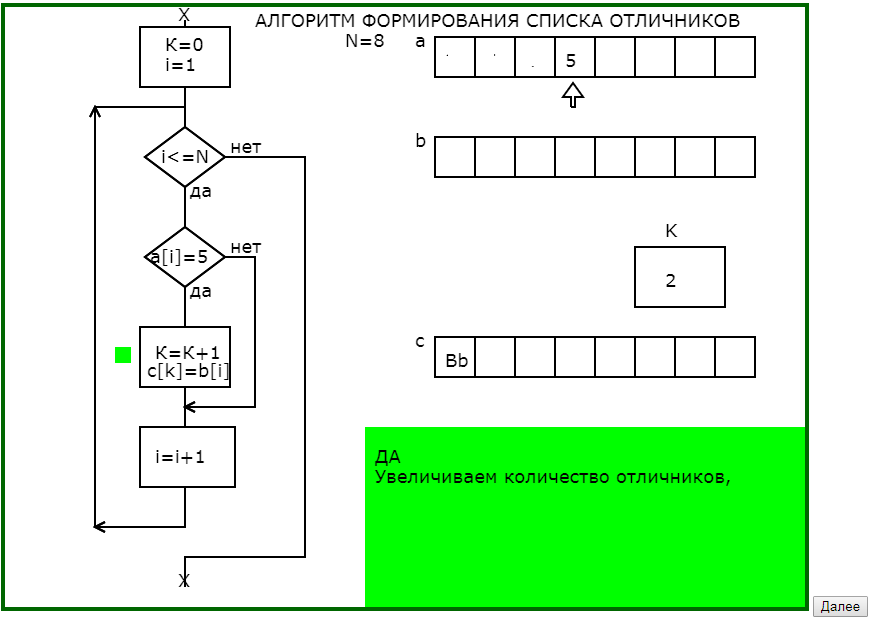
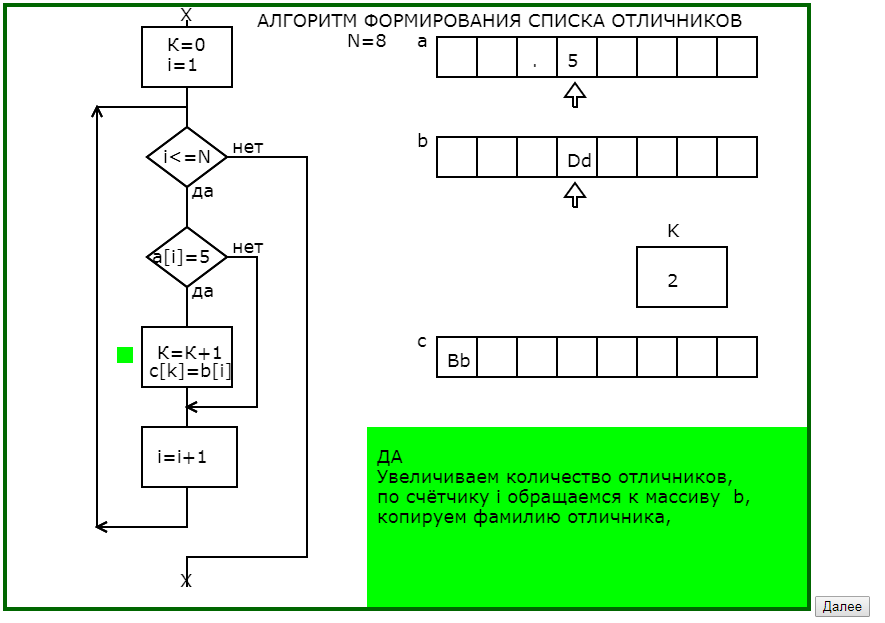
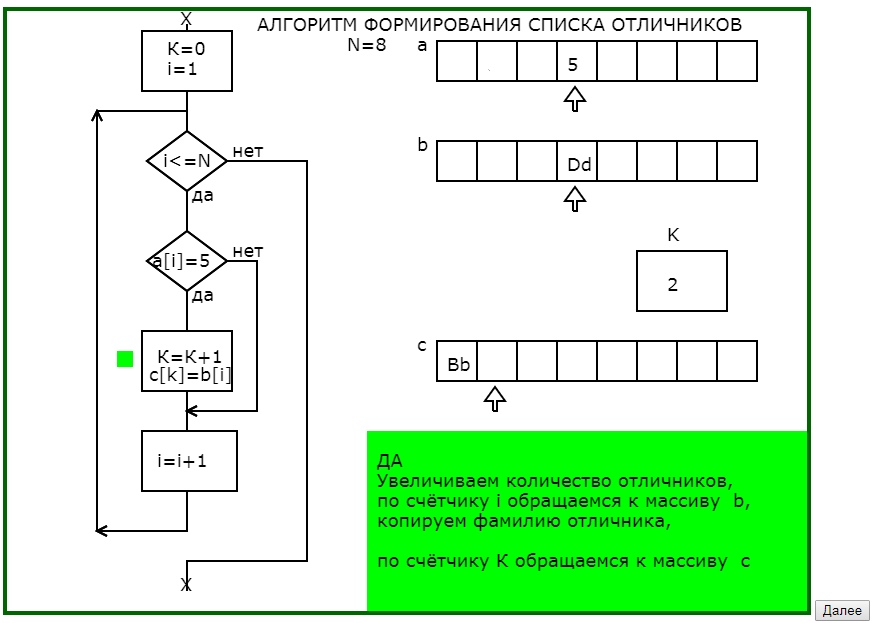
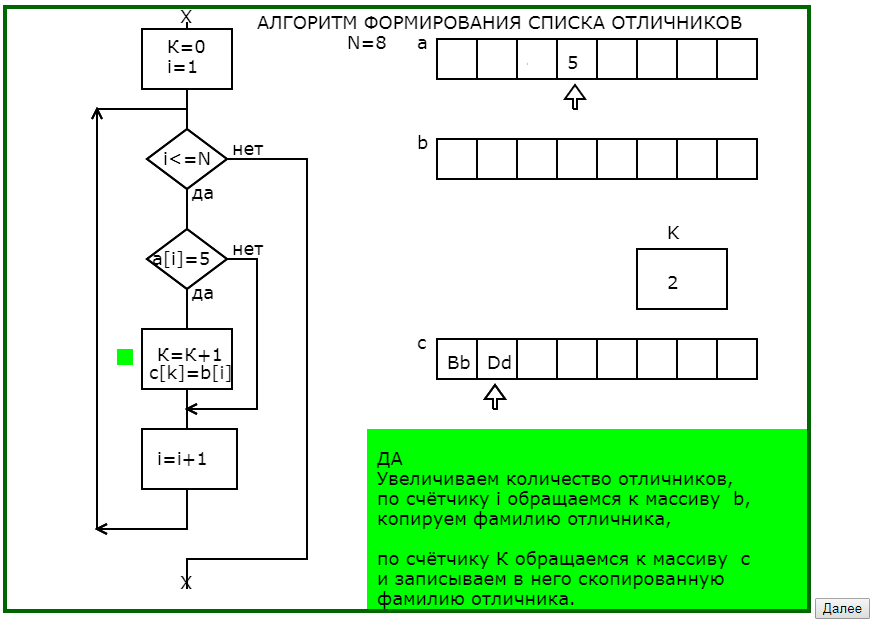Рис.2. Последовательность кадров обучающей программы
«Формирование списка отличников»

Формирование кадра обучающей программы как маленькой WEB-страницы даёт и более широкие возможности создания нового обучающего контента.

Тут и компьютерный эксперимент с возможностью выбора пути прохождения обучающей программы, и получение подсказок, и формирование и проверка гипотез и многое другое.

Конечно, построение этаких программ трудоёмко, но эффект их применения стоит того.

Исходные тексты алгоритмов в архиве (формат zip)

Литература:
1. Шаталов В. Ф и др. Опорные конспекты по кинематике и динамике: Кн. для учителя: Из опыта работы / В. Ф. Шаталов, В. М. Шейман, А. М. Фаит. М.: Просвещение, 1989. с. 15
2. Зенкин.А.А. Когнитивная компьютерная графика. Применение в классической теории чисел. — М.: Наука, 1991, 191 стр.
3. Бочанова Н.Н. Основы программирования в динамических опорных сигналах, Часть 1. Азбука программирования – Курск, КГТУ, 1995,  354 с.
4. Педагогическая модель  алгоритма подсчёта элементов массива, удовлетворяющих заданному условию, Бочанова Н.Н. , Аникина Е.И. // Свидетельство о государственной регистрации программы для ЭВМ №2016614118, Российская Федерация, заявл.24.02.2016, зарегистрировано 14.04.2016
5. Педагогическая модель трассировки алгоритма подсчёта элементов массива, удовлетворяющих заданному условию: Бочанова Н.Н., Аникина Е.И //Свидетельство о государственной регистрации программы для ЭВМ №2016614117, Российская Федерация, заявл.24.02.2016, зарегистрировано 14.04.2016
6. Модуль электронного учебника-тренажёра для поиска ошибок в алгоритмах: Бочанова Н.Н., Бурыкина А.Д. //в сборнике Программная инженерия: современные тенденции развития и применения, сборник материалов Всероссийской конференции. 2017.с.5-9