Школа программирования ProgTips В данной статье мы познакомимся с различными видами комплексных фракталов и способами их отрисовки с помощью библиотек GTK и Cairo.
Почему эти фракталы называются комплексными? Очень просто: для их получения используются комплексные числа.
Понятие комплексного числа появилось в результате развития теории решения квадратных уравнений с отрицательным дискриминантом. Математикам пришлось освоить новую идею о том, что некоторые величины возведённые в чётную степень могут давать отрицательные значения. Так в математику вошла мнимая единица, квадрат которой даёт минус единицу. Что же представляет собой комплексное число?
Согласно стандартному определению: комплексное число это выражение вида
в котором a и b принадлежат множеству действительных чисел, а i это мнимая единица. Говоря простым языком: комплексное число это сумма двух чисел — вещественного (a) и мнимого (b).
Так же как и для любых других чисел, для комплексных чисел определены свои правила сложения, умножения, деления, вычитания и возведения в степень. Комплексным числам как математическому понятию посвящено очень много литературы. Вкратце с необходимой информацией можно ознакомиться например здесь.
Комплексные числа часто встречаются в инженерной практике, так как позволяют в удобной форме работать с представлениями сигналов. Так же эти числа можно встретить и высокой науке, такой как теория относительности. Математика комплексных чисел используется практически во всех программах предназначенных для обработки музыки и звука. Так что очень полезно узнать об этих числах как можно больше, если вы хотите заниматься чем-то подобным.
Ну и конечно же эти числа применяются в области компьютерной графики для получения красивых фрактальных изображений. Как уже было сказано ранее, на заре компьютерной графики, Бенуа Мандельброт был первым, кто применил комплексные числа для получения фрактальных изображений. И мы начнём наш экскурс с рассмотрения фрактала названного в его честь. Но так как мы будем рассматривать множество различных фракталов, то лучше всего будет, если мы сразу подготовим архитектуру нашего приложения.
Архитектура приложения
В предыдущей статье мы использовали GTK для создания окна и области рисования и далее работали с этой областью. В нашем случае мы оставляем всё как есть и просто расширяем имеющийся функционал, добавляя в него необходимые для нашей задачи методы. Так как мы пишем генератор фрактальных изображений, нам нужно добавить небольшую панель, на которой мы разместим управляющие элементы. Они позволят нам задавать некоторые параметры, которые будут общими для всех типов рассматриваемых фракталов, а это:
- Координаты центра отрисовки фрактального изображения
- Масштаб отрисовки
- Тип фрактала
Данные параметры можно передать через созданные поля ввода. Соответственно, нам нужно будет также создать кнопку для запуска процесса обновления. Поэтому исходный код drawing_window.php примет следующий вид:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 |
<?php abstract class FractalDrawingWindow extends GtkWindow { // Передаваемые параметры var $centerX = 0.; // положение центра отрисовки var $centerY = 0.; var $scale = 1.; // масштаб var $ftype = 0; // тип фрактала (объяснение будет дано далее) public function FractalDrawingWindow() { parent::__construct(); $this->set_title($this->getName()); $this->connect_simple('destroy', array('gtk', 'main_quit')); $this->connect('key-press-event', array($this, 'onKeyPress')); $drawingArea = new GtkDrawingArea(); $drawingArea->connect('expose_event',array($this,'onExpose')); $drawingArea->set_size_request(640,480); // здесь мы создаём три заголовочных элемента для обозначения параметров $labelCenter = new GtkLabel('Center',true); $labelScale = new GtkLabel('Scale', true); $labelType = new GtkLabel('Type', true); // здесь мы создаём элементы для ввода информации по параметрам $textCenterX = new GtkEntry(strval($this->centerX)); $textCenterY = new GtkEntry(strval($this->centerY)); $textScale = new GtkEntry(strval($this->scale)); // для выбора типа фрактала мы используем текстовый комбобокс $comboType = GtkComboBox::new_text(); // так как мы не знаем конкретно какие фракталы мы будем использовать, // поэтому просто сделаем вызов виртуального метода, который вернёт нам // список с доступными фракталами foreach($this->getRegisteredFractals() as $fractal){ // и получим их имена, так же используя виртуальный метод $comboType->append_text($fractal->getTypeName()); } $comboType->set_active($this->type); // установим значение по умолчанию // дальше зададим кнопку для обновления изображения $submitButton = new GtkButton('Submit'); // и вешаем на неё обработчик (метод submit) $submitButton->connect('clicked', array($this,'submit'), $drawingArea, $textCenterX, $textCenterY, $textScale, $comboType); // ещё бы не плохо отслеживать процесс получения изображения, // поэтому мы добавим ещё индикатор прогресса $progress = new GtkProgressBar(); // теперь мы можем всё это объединить, создав единую виртуальную панель $vbox = new GtkVBox(false,0); // добавляем на панель область рисования $vbox->pack_start($drawingArea,false,false,0); // за ней следует индикатор прогресса $vbox->pack_start($progress, false, false, 0); // и далее панель управления, заданная в виде таблицы $controlTable = new GtkTable(3,3); // добавляем элементы в таблицу $controlTable->attach($labelCenter, 0,1, 0,1); $controlTable->attach($textCenterX, 1,2, 0,1); $controlTable->attach($textCenterY, 2,3, 0,1); $controlTable->attach($labelScale, 0,1, 1,2); $controlTable->attach($textScale, 1,2, 1,2); $controlTable->attach($labelType, 0,1, 2,3); $controlTable->attach($comboType, 1,2, 2,3); $controlTable->attach($submitButton, 2,3, 1,3); // присоединяем таблицу к панели $vbox->pack_start($controlTable, false,false,0); // теперь можно добавить панель к окну $this->add($vbox); $this->set_position(GTK::WIN_POS_CENTER); // нам обязательно нужно повесить обработчик на наш индикатор прогресса Gtk::timeout_add(200,array($this,'updateProgress'), $progress); // он будет вызваться раз в 200 мс в основном потоке приложения // показываем все элементы $this->show_all(); } // эта функция как и прежде показывает изображение фрактала function onExpose($drawingArea, $event){ $context = $drawingArea->window->cairo_create(); $this->onDraw($context); } // эта функция реагирует на нажатие клавиши q (выход) function onKeyPress($widget, $event){ if ($event->keyval == Gdk::KEY_q) { $widget->destroy(); } } // здесь мы передаём параметры из интерфейса в наш класс function submit($widget, $drawingArea, $textCenterX, $textCenterY, $textScale, $comboType){ $this->centerX = floatval($textCenterX->get_text()); $this->centerY = floatval($textCenterY->get_text()); $this->scale = floatval($textScale->get_text()); $this->ftype = intval($comboType->get_active()); $this->set_title($this->getName()); // меняем название окна $drawingArea->queue_draw(); // и запускаем перерисовку (onExpose) } // обновляем состояние прогресса function updateProgress($progress){ $progress->set_fraction($this->getState()); return true; } // элементарные гетеры (методы для получения параметров фрактала) public function getCenterX(){ return $this->centerX; } public function getCenterY(){ return $this->centerY; } public function getScale(){ return $this->scale; } public function getFType(){ return $this->ftype; } // объявление абстрактных методов abstract public function getState(); // получение состояния отрисовки фрактала abstract public function getName(); // получение имени рисуемого фрактала abstract public function getRegisteredFractals(); // получение списка доступных фракталов abstract protected function onDraw($context); // метод отрисовки } ?> |
Теперь мы должны унаследоваться от данного класса и определить конкретный вид указанных абстрактных методов. В целом мы хотим получить возможность рисовать фракталы разных видов, используя общий для всех фракталов алгоритм. Поэтому я должен объяснить в чём он заключается.
Метод получения фрактального изображения основан на итерировании одной и той же комплексной формулы. По сути это рекурсивный вызов функции с параметром полученным на предыдущем шаге. Но так как мы уже постигли кое-что относительно рекурсии, мы будем использовать именно итерации, так как в этом случае код будет довольно простым и эффективным. Для каждого отдельного вида фрактала формула будет своя, но в то же время она будет общей для всего множества пикселов принадлежащих данному виду фрактала. И в то же время алгоритм прохода по всем пикселам изображения (всей комплексной плоскости) будет общим для всех типов фракталов и мы реализуем его в единственном экземпляре.
Итак всё что мы хотим это пройтись по всему множеству точек фрактала, посчитать в них значения интенсивности, и далее сделать небольшое улучшение полученного изображения, а затем отобразить его в нашем окне. Думаю будет неплохо использовать случайным образом сгенерированные градиенты и альфа-смешивание, чтобы можно было увидеть красоту фрактала «в цвете».
Теперь мы можем приступать к написанию основного класса нашего приложения fractal_drawer.php.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 |
<?php include 'drawing_window.php'; // нам потребуется создать отдельный файл для каждого вида фрактала require_once 'mandelbrot_set.php'; require_once 'julia_set.php'; require_once 'newton_fractal.php'; require_once 'nova_fractal.php'; require_once 'rational_map.php'; require_once 'glynn_fractal.php'; class FractalDrawer extends FractalDrawingWindow { // обозначаем статический массив для хранения объектов для генерации // конкретного типа фрактала private static $types = array(); // ещё создадим переменную для хранения текущего состояния отрисовки var $progress = 0.0; public function FractalDrawer(){ // регистрация типов фракталов должна происходить перед инициализацией интерфейса $this->registerFractals(); // поэтому мы взываем родительский конструктор после вызова метода регистрации parent::__construct(); } // метод регистрации всех видов фракталов public function registerFractals(){ // соответственно мы просто создаём по одному объекту для каждого типа фрактала self::$types = array( new MandelbrotSet(), new JuliaSet(), new NewtonFractal(), new NovaFractal(), new RationalMap(), new GlynnFractal() ); } // метод получения зарегистрированных типов фракталов public function getRegisteredFractals(){ if(self::$types == null){ // если они по какой-то причине регистрировалась, то производится сначала эта процедура $this->registerFractals(); } return self::$types; } // метод возвращает текущий используемый объект-генератор фрактала public function getFractal(){ return $this->getRegisteredFractals()[$this->ftype]; } // метод даёт имя текущего используемого объекта-генератора public function getName() { return $this->getFractal()->getTypeName()." fractal"; } // получить текущее состояние выполнения генерации изображения public function getState(){ return $this->progress; } // установить текущий уровень прогресса генерации изображения public function setProgress($state){ $this->progress = $state; } // метод генерации фрактала (общий для всех видов фракталов) protected function genFractal(){ $width = floatval($this->get_size()[0]); // получение размера изображения $height = floatval($this->get_size()[1]); // далее идут предварительные вычисления для упрощения записи и вычислений $div = $width; if($height < $width) $div = $height; $div = 1./($div*$this->getScale()); $scale = 1./$this->getScale(); $depth = 128; $maxin = 255; $coef = floatval($maxin + 1)/ $depth; $centerXscale = $this->getCenterX()*$scale; $centerYscale = $this->getCenterY()*$scale; // создаём массив байт изображения $bytes = array($height*$width*4); for($y = 0.; $y < $height; $y++){ // шагаем по вертикали $this->setProgress($y / $height); // обновляем статус обработки изображения for($x = 0.; $x < $width; $x++){ // шагаем по горизонтали $val = $this->getFractal()->getValue($x*$div + $centerXscale,$y*$div + $centerYscale, $depth); // делаем зум, смещение и получаем интенсивность писксела // делаем небольшую коррекцию if($val != $depth) $val *= $coef; else $val = 255; // далее записываем результат for($k = 0; $k < 3; $k++){ $bytes[$y*$width*4+$x*4+$k] = $val; // RGB-значения интенсивности } $bytes[$y*$width*4+$x*4+3] = 0; // альфа-канал } } // теперь осталось создать поверхность с изображением фрактала $str_surface=implode(array_map("chr",$bytes)); $surface = cairo_image_surface_create_for_data($str_surface, CAIRO_FORMAT_ARGB32 , $width, $height); // функция требует на вход объект типа string return $surface; } // метод генерации простенького градиента protected function getGradient($type, $color1, $color2){ $gradientPattern = null; $width = $this->get_size()[0]; $height = $this->get_size()[1]; if($type == 0){ // линейный градиент $gradientPattern = new CairoLinearGradient(0,0,0,$height); // здесь просто указываются координаты начала и конца отрезка для протяжки } else { // радиальный градиент $gradientPattern = new CairoRadialGradient($width/2,$height/2,$height/2, $width/2, $height/2, $width); // здесь мы указываем координаты и радиусы цветовых кругов } // устанавливаем значения цвета $gradientPattern->addColorStopRGBA(0, $color1[0], $color1[1], $color1[2], $color1[3]); //... // здесь можно добавить больше цветов в промежутке от 0 до 1 для первого параметра $gradientPattern->addColorStopRGBA(1, $color2[0], $color2[1], $color2[2], $color2[3]); return $gradientPattern; } // главный метод protected function onDraw($context){ // здесь мы всё объединяем $this->setProgress(0.0); // генерируем фрактал $fractalSurface = $this->genFractal(); // генерируем случайные цвета $r1 = mt_rand() / mt_getrandmax(); $g1 = mt_rand() / mt_getrandmax(); $b1 = mt_rand() / mt_getrandmax(); $r2 = mt_rand() / mt_getrandmax(); $g2 = mt_rand() / mt_getrandmax(); $b2 = mt_rand() / mt_getrandmax(); $gradType = rand(0,2); // получаем случайный градиент $gradientPattern = $this->getGradient($gradType,array($r1,$g1,$b1,1),array($r2,$g2,$b2,1)); // и смешиваем их $context->setSource($gradientPattern); $context->paint(); $context->setOperator(CAIRO_OPERATOR_OVER); // вот здесь можно указать и другие операторы для смешивания (какие именно, нужно посмотреть в документацию) $context->setSourceSurface($fractalSurface); $context->paint(); // здесь всё завершается! это очень просто $this->setProgress(1.0); } } // создаём и тестируем наш класс $fractalDrawer = new FractalDrawer(); Gtk::main(); ?> |
Так как в функции onDraw мы используем один и тот же метод getValue, то будет разумным, создать отдельный абстрактный класс интерфейса, общий для всех видов фракталов. Мы назовём его FractalSet и создадим для него отдельный файл fractal_set.php. Это позволит нам удобно обращаться с фракталами в не зависимости от их конкретного вида. В классе будет всего два метода, поэтому он будет выглядеть достаточно лаконично:
|
1 2 3 4 5 6 |
<?php abstract class FractalSet{ abstract public function getTypeName(); abstract public function getValue($re0, $im0, $depth); } ?> |
Теперь всё готово для того, чтобы приступить к рассмотрению отдельных видов фракталов.
Фрактал Мандельброта
Итак, в предыдущих статьях мы уже встречались с данным видом фрактала. Вы даже можете увидеть его изображение на одной из фотографий, которые были приведены в статье . Этот фрактал является иконой фрактальной графики. Он бесконечно сложен и в то же время очень красив и элегантен. А с точки зрения математики алгоритм его получения весьма прост и определяется формулой:
Здесь n это номер итерации, а с — произвольная константа (обычно за неё принимают текущие координаты на комплексной плоскости). Начальные условия у нас такие:
Итерирование данной формулы при заданном значении константы даёт нам величину интенсивности по номеру итерации, при условии что получаемая точка не выходит дальше области ограниченной окружностью радиуса 2. Этот алгоритм реализуется в следующем коде:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
<?php require_once 'fractal_set.php'; class MandelbrotSet extends FractalSet{ public function getTypeName(){ return "Mandelbrot"; } // получение значения интенсивности изображения фрактала в точке (re0, im0) public function getValue($re0, $im0, $depth){ // действие происходит на комплексной плоскости // здесь мы задаём начальные координаты $z_re = 0.0; // соответствует положению на оcи X $z_im = 0.0; // Y, соответственно /* * Итеративный процесс поиска решения */ $i = 0; while($i < $depth){ // процесс завершается при достижении максимальной глубины итерации // вычисляем квадраты значений компонент комплексной переменной $re2 = $z_re*$z_re; $im2 = $z_im*$z_im; // проверяем условие выхода точки за пределы круга с радиусом 2 if ($re2 + $im2 >= 4.0) return $i; // возвращаем интенсивность по номеру итерации // вычисляем новую точку по значению предыдущей $z_im = 2.0*$z_re*$z_im + $re0; $z_re = $re2 - $im2 + $im0; // здесь и содержится основная формула преобразования координат во фрактальное изображение // формула, по которой мы можем идентифицировать тот или иной фрактал // инкрементируем счётчик итерации $i += 1; } return $depth; // возвращаем максимальную интенсивность } } ?> |
В нашем случае, запуск fractal_drawer.php приведёт к созданию самоподобной красоты:
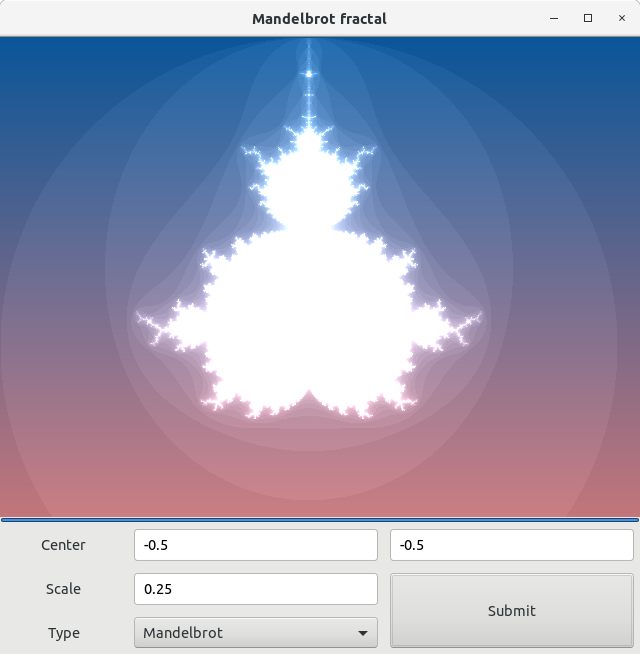
Существуют различные вариации данного вида фрактала. Особенно изысканным в среде дизайнеров считается вариант имеющий название Buddhabrot и напоминающий сидящего в позе лотоса медитирующего будду. Получить его значительно труднее, поэтому я предлагаю выполнить это в качестве упражнения, которое расширит ваше сознание, подобно тому как это делал сам будда.
Ну а мы переходим к следующему виду фрактала, получившего название в честь французского математика Гастона Жюлиа, так горячо любимого самим Мандельбротом.
Фрактал Жюлиа
Начальные условия:
Здесь подход немного отличается от представленного выше. Теперь мы используем константу как константу в том смысле, что её значение не будет меняться. А итерации мы начнём с той точки, которая задана через параметры метода.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
<?php require_once 'fractal_set.php'; // существует множество различных вариаций данного вида фрактала const JuliaConstants = array( 'common' => array(-0.7,0.2), 'golden' => array(-0.618, 0.0), 'stars' => array(-0.70176,0.3842), 'lightning' => array(0.0,-0.8), 'rabbit' => array(-0.123,0.745), // мне например нравиться этот ); class JuliaSet extends FractalSet{ // здесь мы задаём константу, определяющую внешний вид фрактала var $const_re; var $const_im; public function JuliaSet($name = 'common'){ $this->const_re = JuliaConstants[$name][0]; $this->const_im = JuliaConstants[$name][1]; } public function getTypeName(){ return "Julia"; // Жульё, как говориться } // всё тоже самое, что и во множестве Мандельброта, за исключением интерпретации параметров public function getValue($re0, $im0, $depth){ $z_re = $re0; // теперь мы начинаем с точки (re0, im0) $z_im = $im0; $i = 0; while($i < $depth){ $re2 = $z_re*$z_re; $im2 = $z_im*$z_im; if ($re2 + $im2 >= 4.0) return $i; $z_im = 2.0*$z_re*$z_im + $this->const_im; // и используем константу $z_re = $re2 - $im2 + $this->const_re; // как константу $i += 1; } return $depth; } } ?> |
У меня получился такой вариант:
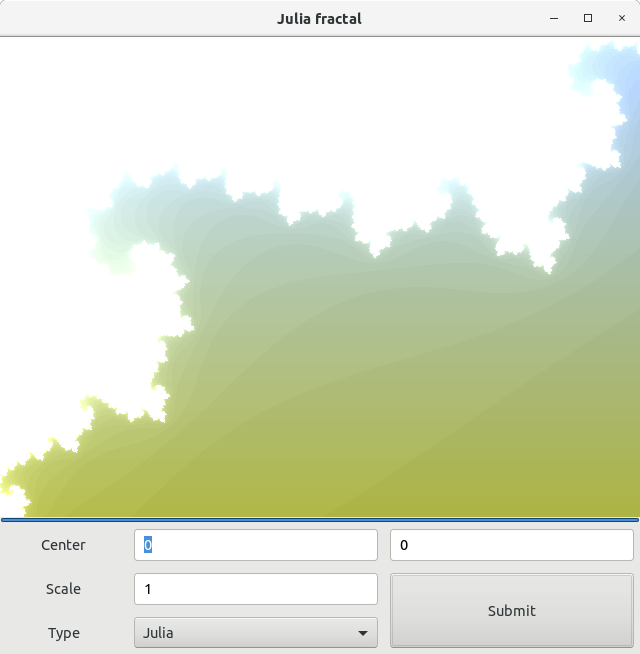
Выглядит немного мистически и загадочно. Вариаций данного фрактала тоже очень много, вы можете поиграться с параметрами, чтобы убедиться в этом. А следующим видом фракталов мы рассмотрим фрактал, названный в честь великого английского физика и астронома — Исаака Ньютона.
Фрактал Ньютона
Вид функции f(z) может быть любой, в частности мы будем использовать следующую функцию:
Здесь функция в знаменателе это производная от функции f(z), то есть
И вот здесь начинается самое интересное, потому как ранее мы использовали сравнительно простые формулы из теории комплексных чисел. Так вот, для того, чтобы построить фрактал Ньютона, нам нужно использовать операцию возведения в третью степень, а так же деление. Это может быть сделано несколькими способами, но чтобы не усложнять себе жизнь громоздкими формулами, мы воспользуемся библиотекой Math_Complex, доступной для скачивания из официального репозитория php. Вы можете установить её с помощью пакетного менеджера pear или скачать новую версию с github’а. Ну а я просто покажу вам как её использовать для наших целей:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
<?php require_once 'fractal_set.php'; require_once 'Math/ComplexOp.php'; // здесь мы подключаем библиотеку class NewtonFractal extends FractalSet{ public function getTypeName(){ return "Newtonian"; } public function getValue($re0, $im0, $depth){ $z = new Math_Complex($re0,$im0); // теперь мы можем обращаться с z как с настоящим комплексным числом $roots = array(new Math_Complex(1,0),new Math_Complex(-0.5,sqrt(3)/2), new Math_Complex(-0.5,-sqrt(3)/2)); // здесь мы задаём набор констант, являющихся точным решением уравнения, которое мы будем использовать далее // нам нужно определить так же точность, с которой нас устроит приближённое решение, полученное по методу Ньютона $tolerance = 0.0001; // начинаем поиск приближённого решения $i = 0; while($i < $depth){ // здесь мы вычисляем новое значение по методу Ньютона для нашего уравнения $z = Math_ComplexOp::sub($z, Math_ComplexOp::div($this->F($z),$this->Fder($z))); /* * sub это операция вычитания между аргументами, * div это операция деления двух комплексных чисел * функция F и её производная Fder будут раскрыты далее */ // проверяем условие на совпадение точного и приближённого решений foreach($roots as $root){ $diff = Math_ComplexOp::sub($z,$root); // делаем это вычисляя простую разность if($diff->abs()<=$tolerance) return $i; // возвращаем интенсивность, если точность удовлетворяет } $i += 1; } return $depth; // если решение не найдено, то возвращаем максимальное значение интенсивности } // определяем функцию числителя private function F($z){ return Math_ComplexOp::sub(Math_ComplexOp::powReal($z,3), new Math_Complex(1,0)); // здесь мы используем функции вычитания sub и возведения в степень powReal } // определяем функцию знаменателя private function Fder($z){ return Math_ComplexOp::mult(Math_ComplexOp::mult($z,$z),new Math_Complex(3,0)); // здесь мы используем функцию умножения mult } } ?> |
Конечно всё это не эффективно с точки зрения производительности вычислений, потому как под каждой из комплексных операций скрывается очень много ненужных действий, которые можно сократить если вы знаете комплексную математику. В крайнем случае вы можете использовать пакеты символьной алгебры, такие как Maxima или Wolfram Alpha. Это весело, но всё же знание математики необходимо, если вы хотите создавать по-настоящему эффективные приложения.
Насладимся же ещё одним видом прекрасного фрактала…
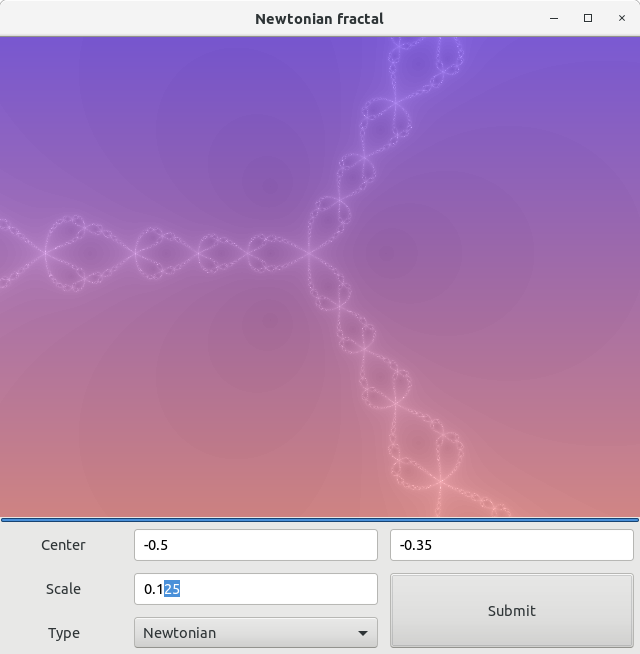
Следующим примером, мы рассмотрим фрактал Nova. Этот фрактал отдалённо напоминает нам свет далёкой звезды, манящей и непостижимой… Как говорил великий Иммануил Кант:
Две вещи наполняют душу всегда новым и все более сильным удивлением и благоговением, чем чаще и продолжительнее мы размышляем о них — это звездное небо надо мной и моральный закон во мне
Фрактал Nova
Удивителен факт, что наши тела состоят атомов рождённых в недрах звёзд. Ещё более удивительно, что элементы без которых мы не можем жить являются посмертным даром звёзды, завершившей цикл своей эволюции и вспыхнувшей в виде сверхновой. Выражаясь поэтически: жизнь и смерть неразрывно связаны между собой, и нечто, умирая, даёт возможность жизни продолжиться в бесконечность…
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
<?php require_once 'fractal_set.php'; class NovaFractal extends FractalSet{ public function getTypeName(){ return "Nova"; } public function getValue($re0, $im0, $depth){ $a = $re0; $b = $im0; // задание констант $ra = 1; // r $rb = 1; $ca = 2; // и c $cb = 1; // задание точности поиска решения $tolerance = 0.001; $a_old = $a + $tolerance; $b_old = $b + $tolerance; $i = 0; while($i < $depth){ // делаем элементарные упрощения $a2 = $a*$a; $b2 = $b*$b; $b4 = $b2*$b2; $a4 = $a2*$a2; $div= $a2+$b2; $div = 3*$div*$div; if($div==0) return $i; // защита от деления на 0 //...в идеальном мире так получают бесконечность $ab2 = $a2*$b2; // к сожалению я не запомнил сохранил изначальной формулы // когда использовал Wolfram Alpha для её упрощения $a -= $ra * ($a2 - $b2 + $a*$b4 + $a4*$a + 2*$a*$ab2)/$div - $ca; $b -= $rb * (-2*$a*$b + $b4*$b + 2*$ab2*$b+$a4*$b)/$div - $cb; //...вот так в потоке бытия забывается всё вечное if(abs($a-$a_old) <= $tolerance && abs($b-$b_old) <= $tolerance) return $i; $a_old = $a; $b_old = $b; $i += 1; } return $depth; } } ?> |
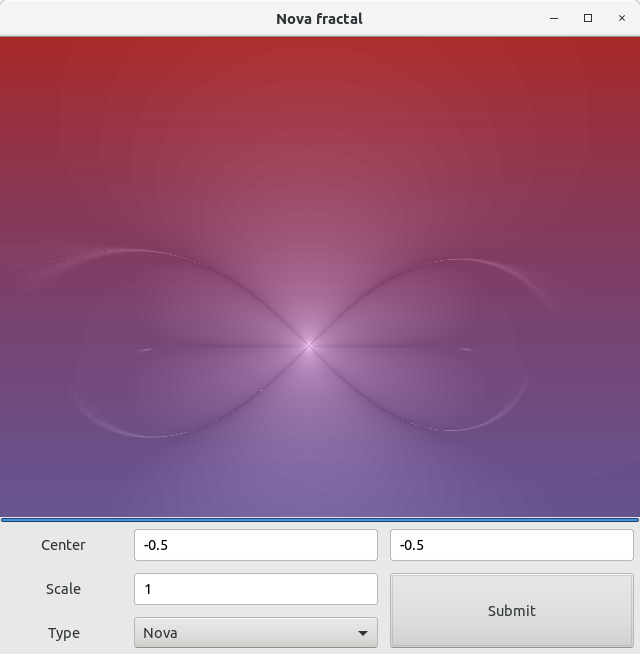Данный фрактал как никакой другой содержит в себе аллюзию к вечности…
И ещё я бы хотел рассмотреть один вид фрактала, о котором я не знаю решительно ничего, кроме того, что он напоминает мне дерево Пифагора.
Фрактал Глина
Подобный фрактал уже встречался нам в статье про основы фрактальной графики. Здесь же он возникает в результате применения итераций над функцией комплексной переменной. То есть здесь дискретный и аналитический миры встречаются и крепко пожимают друг другу руки… или ветви, как там принято у деревьев… Вообщем настоящая пифагорейская гармония, как и должно быть, так вот. Код его предельно прост и не нуждается в комментариях:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
<?php require_once 'fractal_set.php'; require_once 'Math/Complex.php'; // class GlynnFractal extends FractalSet{ public function getTypeName(){ return "Glynn"; } public function getValue($const_re, $const_im, $depth){ $z = new Math_Complex($const_re,$const_im); $c = new Math_Complex(0.1948,0); // константа связанная со знаменательной датой $i = 0; while($i < $depth){ $z = $this->F($z,$c); if($z->abs2() >= 4) return $i; $i += 1; } return $depth; } // очень простая функция private function F($z,$c){ return Math_ComplexOp::sub(Math_ComplexOp::powReal($z,1.5), $c); } } ?> |
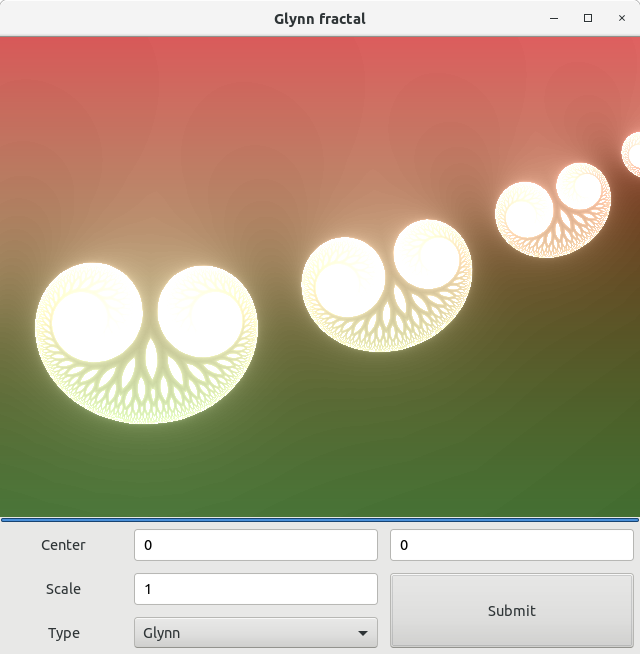
Если немного изменить масштаб, то можно увидеть здесь и другую философскую вещь. А именно, что очертания набора «фрактального леса» напоминает по форме обыкновенное семя, которое по сути содержит в себе потенцию порождения как отдельного дерева, так и обширного леса. Иногда простое изменение точки зрения позволяет видеть более упорядоченную картину, что называется «видеть лес за деревьями». Данная способность является неотъемлемым признаком высокоразвитого интеллекта. Так что занятие над фракталами пойдёт на пользу вашему интеллекту. В качестве упражнения я предлагаю разобраться со следующим видом фрактала самостоятельно.
Фрактал Rational map
Перед вами исходный код этого фрактала:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
<?php require_once 'fractal_set.php'; require_once 'Math/Complex.php'; class RationalMap extends FractalSet{ public function getTypeName(){ return "Rational map"; } public function getValue($const_re, $const_im, $depth){ $roots = array( new Math_Complex(-0.769161,0), new Math_Complex(0,-0.769161), new Math_Complex(0,0.769161), new Math_Complex(0.769161,0) ); $a = $const_re; $b = $const_im; $tolerance = 0.1; $i = 0; while($i < $depth){ $a2 = $a*$a; $b2 = $b*$b; $inv = $a2 - $b2; $div = $a2 + $b2; $div = $div*$div; if($div == 0) return $i; $ab = $a*$b; $a = (-0.35/$div + 1)*$inv; $b = (0.7/$div + 2)*$ab; foreach($roots as $root){ if(abs($root->getReal() - $a) <= $tolerance && abs($root->getIm() - $b) <= $tolerance) return $i; } $i += 1; } return $depth; } } ?> |
Попробуйте сделать так, чтобы этот фрактал выглядел так же красиво, как и все остальные приведённые выше. Подсказка: потребуется сделать изменения в коде, чтобы получить более качественное изображения, потому как в данном коде содержится неявная ошибка, которая не является критической, но всё же может быть устранена.
И ещё, наверное вы заметили, что порой процесс генерации фракталов происходит очень медленно и вызывает замирания пользовательского интерфейса. Я предлагаю вам подумать о том, как обойти это.
Заключение
Что ж и на этом цикл статей по фрактальной графике временно приостанавливается (помните, что фракталы это бесконечная тема). Надеюсь вам было интересно, ну а дальше нас ждёт что-то совершенно особенное… приключение… и об этом в следующей статье, удачи!